La fama di Leibniz come matematico è legata soprattutto alla prima sistemazione organica del «calcolo infinitesimale». Di essa egli diede notizia in due articoli pubblicati negli Acta Eruditorum («Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas, nec irrationales quantitates moratur, et singulare pro illis calculi genus», 1684 e «De geometria recondita et analysi indivisibilium atque infinitorum», 1686). Tale pubblicazione diede origine ad una violenta polemica a distanza con Isaac Newton, il quale rivendicò la priorità della scoperta e giunse praticamente ad accusare Leibniz di plagio. I documenti che possediamo sembrano far capire che entrambi giunsero indipendentemente alla stessa scoperta (formulata solo in termini differenti), che del resto era all'epoca preparata dalla soluzione già nota di diversi casi particolari. Diamo qui, in una forma molto semplificata, un'idea dei problemi che il calcolo infinitesimale affronta e degli strumenti coi quali li risolve.Il presupposto del calcolo infinitesimale è l'elaborazione della geometria analitica da parte di Cartesio, vale a dire della possibilità di tradurre problemi geometrici in problemi algebrici e viceversa. Sul piano cartesiano, infatti, ogni funzione f(x) = y è rappresentata da una linea. Come è noto, i polinomi di primo grado sono rappresentati da linee rette, quelli di grado superiore e le funzioni di altro tipo da linee curve. Proprio in relazione a questo secondo caso sorgono due interessanti problemi. In primo luogo: come calcolare l'area di una figura delimitata da linee curve? Esaminiamo il caso più semplice: quello del trapezoide delimitato dai due assi, da una retta parallela all'asse delle ordinate e da una linea curva di funzione f(x) = y. È facile immaginare un metodo approssimato per calcolare quest'area: basta dividere il trapezoide in sottili rettangoli verticali e sommarne l'area. La base di ognuno di essi sarà parte dell'asse delle ascisse, l'altezza sarà calcolata usando la funzione f(x). Ora, è evidente che quanto maggiore sarà il numero dei rettangoli, tanto più preciso sarà il calcolo dell'area. Ma come calcolare l'area esatta? Bisognerebbe dividere la figura in infiniti rettangoli e sommarne le infinitesime aree. È possibile ciò? In secondo luogo: come calcolare il coefficiente angolare della retta tangente ad un dato punto di una linea curva? Anche qui si può pensare ad un sistema approssimato. Si può scegliere nelle vicinanze dell'ascissa data un'altra ascissa, e calcolare le ordinate corrispondenti. Dividendo la differenza delle due ordinate per la differenza delle due ascisse si avrà -- come è noto -- il coefficiente angolare della retta passante per i due punti così individuati. Non si tratta però di una tangente, perché essa attraversa la linea curva in due punti. Per ottenere il coefficiente della tangente bisognerebbe rendere infinitamente piccola la distanza tra le due ascisse (e di conseguenza tra le due ordinate), e calcolare il quoziente tra due infinitesimi. È possibile?
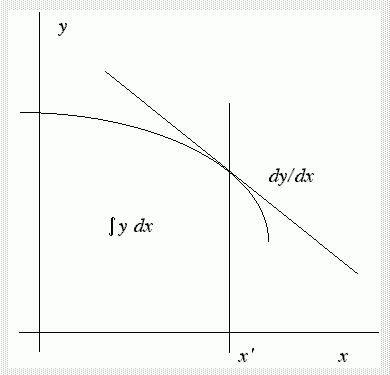
I due problemi fondamentali del calcolo infinitesimale. Qual è il coefficiente angolare della retta tangente in un punto di ascissa x' ad una curva f(x) = y? Qual è l'area del trapezoide delimitato dai due assi, dalla retta x = x' e dalla curva f(x) = y?
2.2. Il calcolo differenziale e integrale
Il problema della tangente venne risolto con quello che Leibniz chiamò «calcolo differenziale». Con esso viene ricavata dalla funzione data y una funzione dy/dx (detta «rapporto differenziale», da leggere «de ipsilon su de ics»), dove la d è un operatore che indica il «differenziale» ovvero l'«incremento infinitesimo» delle variabili. Tale funzione esprime dunque il coefficiente angolare della retta tangente al punto di ascissa x della funzione originaria. Nel caso dei polinomi sono sufficienti due semplici regole:
d(y + z) / dx = dy / dx + dz / dx
d(axn) / dx = anxn-1
La prima regola stabilisce che il differenziale di una somma è uguale alla somma dei differenziali degli addendi: in un polinomio quindi si tratta semplicemente di differenziare separatamente ogni termine. La seconda regola indica quale sia il rapporto differenziale di un monomio. Si noti che essa è valida anche nel caso di costanti (che vanno considerati monomi di grado nullo) e di monomi con esponente negativo o frazionario. Benché la dimostrazione di queste due regole sia relativamente facile, la loro scoperta in termini così generali fu senza dubbio geniale.
Riguardo alla notazione e alla terminologia, abbiamo usato quasi esattamente quella di Leibniz, che era sempre molto attento alla necessità di elaborare simboli comodi e coerenti. Essa è ancor oggi (con poche modifiche) usata, quantunque sia stata abbandonata la teoria intuitiva degli «infinitesimi» che le stava alla base. Il simbolo dx rimane così solo una comoda indicazione della variabile indipendente rispetto a cui bisogna differenziare la funzione (e anche un omaggio a Leibniz). Ai termini «rapporto differenziale» e «differenziare» vengono però oggi preferiti «derivata» e «derivare», che risalgono a Joseph-Louis Lagrange (1736-1813), che adoperò per primo anche il simbolo y' (oggi largamente usato) per indicare la derivata di y.
La situazione è simile per quanto riguarda il problema dell'area. Il procedimento qui introdotto venne chiamato da Leibniz «calcolo integrale». Con esso dalla funzione data y viene ricavata una funzione Sy dx (detta «integrale», da leggere «integrale di ipsilon de ics»), in cui il simbolo S è una esse allungata che simboleggia la somma degli infiniti prodotti degli infinitesimi incrementi dell'ascissa per le ordinate corrispondenti. L'integrale dunque esprime, per ogni valore della funzione originaria, l'area del trapezoide delimitato nel modo prima descritto. Anche in questo caso per i polinomi bastano due semplici regole:
S (y + z) dx = Sy dx + Sz dx
S (axn) dx = ax (n + 1) / (n + 1)
Ecco un esempio di calcolo differenziale e e uno di calcolo integrale:
d (x3 - 3x2 + 4) dx = 3x2 - 6x.
S (2x3 - 4x + 2) dx = x4 / 2 + 2x2 + 2x.
2.3. Il teorema fondamentale
La scoperta forse più importante di Leibniz è che i due problemi ora considerati sono strettamente legati, al punto che differenziazione e integrazione sono operazioni inverse: questo viene chiamato il «teorema fondamentale» del calcolo infinitesimale. Ciò può essere osservato già nelle regole per i polinomi prima presentate. In termini simbolici:
(d Sy dx) / dx = y
S (dy / dx) dx = y + c
Nella seconda espressione, la c indica che l'equivalenza è vera a meno di una costante, come può essere facilmente verificato anche intuitivamente.
Questo teorema fondamentale aiuta a chiarire alcune importanti applicazioni del calcolo infinitesimale nella fisica. Data la funzione che esprime lo spostamento di un corpo in dipendenza del tempo, la derivata rappresenta la velocità, la derivata della velocità (ovvero la «derivata seconda» dello spostamento) rappresenta l'accelerazione. Inversamente, data la funzione che esprime l'accelerazione in dipendenza del tempo, l'integrale del tempo rappresenta la velocità, l'integrale della velocità rappresenta lo spostamento. La celebre formula s = 1/2 gt2 (scoperta già da Galilei) è dunque un semplice integrale secondo della funzione f(t) = g. Queste applicazioni fisiche furono il punto di partenza della sistemazione del calcolo infinitesimale operata da Newton. In suo onore in tali casi si usa ancora la simbologia che egli elaborò, in cui la derivata («flussione», diceva Newton) è indicata da un punto sopra la variabile. Nella matematica contemporanea il «calcolo infinitesimale» viene per lo più spiegato prescindendo dall'idea intuitiva di «infinitesimo» e usando invece il concetto più facilmente definibile di «limite» (al nome di «calcolo infinitesimale» viene di conseguenza preferito quello di «analisi», introdotto nell'uso soprattutto da Leonhard Euler [1707-1783]). Questa diversa interpretazione, anticipata da Jean Le Rond d'Alembert (1717-1783) nella celebre Encyclopédie e resa rigorosa da Augustin-Louis Cauchy (1789-1857), fa evidentemente vacillare le conseguenze metafisiche che Leibniz credeva di poter trarre. Bisogna però anche ricordare che il problema del «continuo», che Leibniz affrontò in connessione con il calcolo infinitesimale, è ancora oggi di grande attualità e per diversi aspetti insoluto. Inoltre, negli anni '60 il matematico Abraham Robinson (Non-standard Analysis, North-Holland, Amsterdam 1966) mostrò come fosse possibile dare un fondamento rigoroso all'idea di infinitesimo, partendo da alcuni sviluppi della teoria dei «numeri transfiniti» di Georg Cantor (1845-1918), un matematico che come Leibniz sostenne l'esigenza di ammettere l'infinito attuale.